プラトン立体とは、五つしか存在しない正多面体の総称です。
・全ての辺の長さが同じ
・全ての面が同一の正多角形で出来ている
・面と面との間に出来る内角の角度がみな等しい
・全ての頂点が内壁に触れるように球体内部に収めることが出来る
という4つの特徴を併せ持つ均衡のとれた形です。
具体的にはどのようなものがあるかといいますと、
① 正四面体(同じ大きさの正三角形4個で出来ている)
② 正八面体(ピラミッドを底面で2つ合わせたような形をしていて、同じ大きさの正三角形8個で出来ている)
③ 正二十面体(同じ大きさの正三角形20個で出来ている)
⇑ここまでは正三角形で囲まれた形
④ 正六面体/立方体(同じ大きさの正方形6個で出来ている)
⑤ 正十二面体(同じ大きさの正五角形12個で出来ている)
5種類しかない希少な正多面体の内の3種類が、正三角形で囲まれた形であるというのは興味深いです。
また、正三角形で出来ているプラトン立体は歪みずらいという特徴を持っていますが、
それとは逆に、正方形と正五角形で出来ている立方体と正十二面体はどちらも
ぐにゃぐにゃとしたフレキシビリティーの高い構造となっています。
その違いにもまた、興味をそそられます。
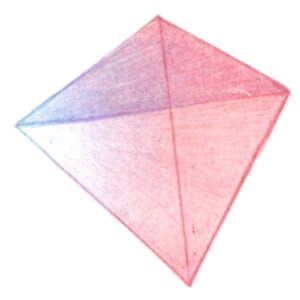
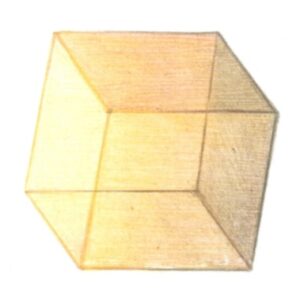
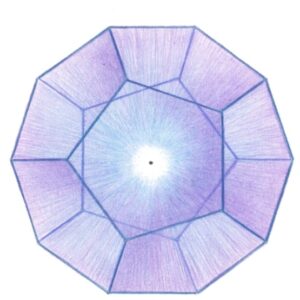
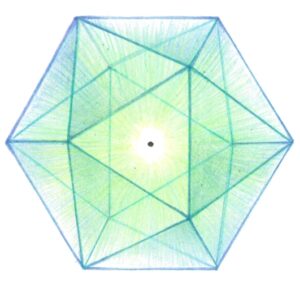
正四面体 正方形 正八面体 正十二面体 正二十面体
正六角形、正七角形、正八角形…を用いたプラトン立体が存在しない理由は?
平たいタイルを思い浮かべてみて下さい。面の形が正六角形のタイル場合、
一つの頂点の周りに3個並べたら隙間なくぴったりとはまってしまいます。
そのために、接合した辺の部分を折って立ち上げて立体を作ろうと思っても不可能です。
全く動かせず、平面にしかなりません。
正七面体や正八面体の場合は、一つの頂点の周りに3個並べることも出来ずに重なり合ってしまいます。
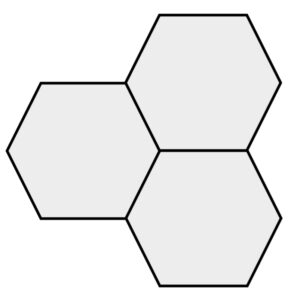
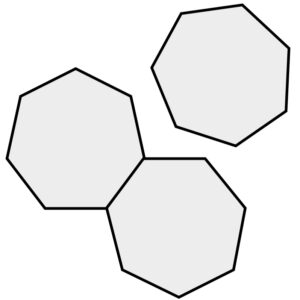
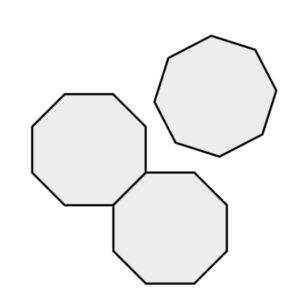
正六角形 正七角形 正八角形
正三角形を用いたプラトン立体が3種類しかないのはなぜ?
正三角形の場合は、6個を一つの頂点の周りに並べると隙間なく並んで正六角形になってしまいます。
これでは、単体の正六角形の場合と同様に平面を埋めるだけです。
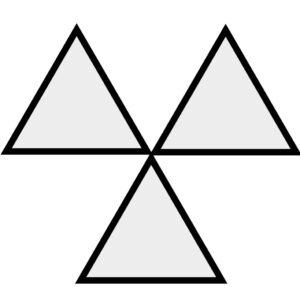
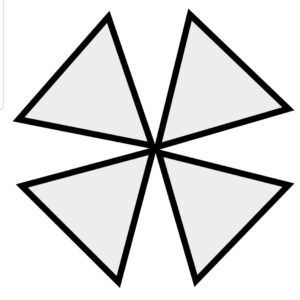
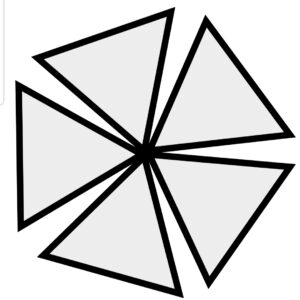
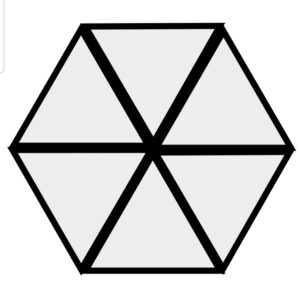
正三角形×3 正三角形×4 正三角形×5 正三角形×6
正四面体の頂点 正八面体の頂点 正二十面体の頂点
立体を形作るためには隙間が必要ですので、一つの頂点に集まる正三角形の数は
3、4、5のいずれかにしかならないのです。
一つの頂点に正三角形が3個集まって正四面体、4個で正八面体、そして5個で正二十面体となります。
正方形と正五角形を用いたプラトン立体の場合は?
立方体の頂点には正方形が3個。正十二面体の頂点には正五角形が3個。
どちらもそれ以上では立体となることが不可能です。
理由はもうおわかりですね。
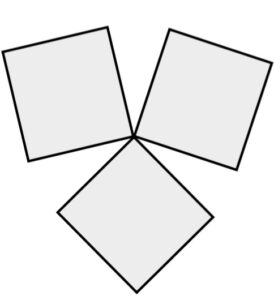
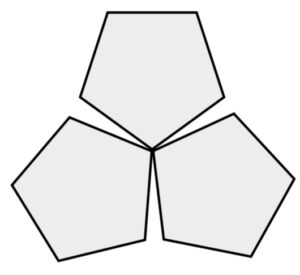
正方形×3 正五角形×3
立方体の頂点 正十二面体の頂点
同じくらいの大きさで描かれることの多いプラトン立体ですが、辺の長さを同じにした場合、
大きさはそれぞれ異なります。
正四面体⇒正八面体⇒立方体⇒正二十面体⇒正十二面体⇒中空の球体
の順で大きくなっています。
プラトン立体の大きさなどはあまり気に留めない方々も多いのでしょうが、
こういったことの中に大切な真実が隠されていたりもします。
ですので、宝探しゲームのように、たまには暗号を解いていくことを楽しんでみることもお勧めです。
元素とプラトン立体
火、土、風、水の四大エレメンツにエーテルを加えた5つの元素がプラトン立体に対応しているとの考え方もあります。
① 正四面体=火
② 正六面体/立方体=土
③ 正八面体=風
④ 正十二面体=エーテル(プラーナやエネルギー、気など、五感ではとらえきれないもの)
⑤ 正二十面体=水
これに6つ目の要素として球=虚空(無)が加えられる場合もあるようです。
球を含めるのは、プラトン立体が球から派生し個性を持つようになったものであるからなのかもしれません。
双対関係
プラトン立体の中には、双対と呼ばれるお互いに非常に関係の深い形どうしが存在します。
プラトン立体を形作る各面の中心を頂点として直線で繋ぎ合わせると、別のプラトン立体になるのです。
そして、新たに出来たプラトン立体の各面の中心を頂点として直線で繋ぎ合わせると、
初めのプラトン立体と同様の形になります。
二つの形が交互に、永遠に拡大縮小して現れる関係性。双対とはこのような関係なのです。
大きな立方体を思い浮かべてみて下さい。
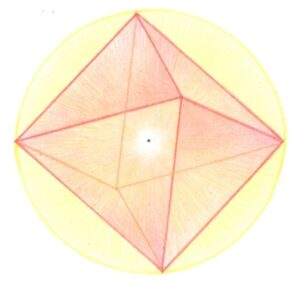
各面を構成している正方形の中心を頂点として、それぞれの点を結び合うと見えてくるのは正八面体になりますね。
その正八面体の各面を構成している正三角形の中心を頂点として直線で結び合うと、今度は立方体になります。
立方体と双対関係になるのは正八面体なのです。
これと同様に、正十二面体と正二十面体も双対関係となっています。
正四面体の場合は同じ正四面体と双対の関係になりますが、これは特別に自己双対と呼ばれています。
大きな上向きの正四面体の各面の中心を頂点として線で繋ぐと下向きの正四面体となりますし、
その下向きの正四面体の各面の中心を頂点として直線で繋ぐと、今度は上向きの正四面体が現れます。
立方体⇔正八面体
正十二面体⇔正二十面体
正四面体⇔正四面体(自己双対)
このように、プラトン立体はお互いに深く関係し合っているのです。
